https://www.acmicpc.net/problem/14285
| Solved.ac 난이도 : P5 |
걸린 시간 : 약 20분
🏷️ 최단 경로
어떤 알고리즘을 알고 있을 경우 체감 난이도가 확 내려가는 류의 문제를 풀 때마다 문제의 난이도가 절대적일 수가 없다는 생각을 종종 하곤 한다. 이 문제의 경우에도 문제를 읽자마자 '최단 경로 다익 짜면 끝이네' 의 생각이 금방 떠오른다. 발상의 아이디어는 거의 없는데 그래프에서 최단 경로 구하는 게 G1이라 문제 난이도가 P5가 되버리는. 최단 경로 빼면 실제 체감 난이도는 실버급..
풀이

일단 $s$와 $t$가 연결된 상황에서 지울 수 있는 간선의 가중치 합의 최댓값을 생각해보자.
이러면 우리는 $s$와 $t$의 최단 경로에 포함되는 간선을 제외한 모든 간선을 지우면 됨을 알 수 있다.
문제에서는 여기서 $s$와 $t$를 연결되지 않도록 하나의 간선을 더 지울 수 있게 해준다. 그러면 우리는 앞에서 구한대로 최단 경로만 남기고 다 지운 후에 최단 경로에서 가장 가중치가 큰 간선만 지우면 될까? 다음 예시를 살펴보자.
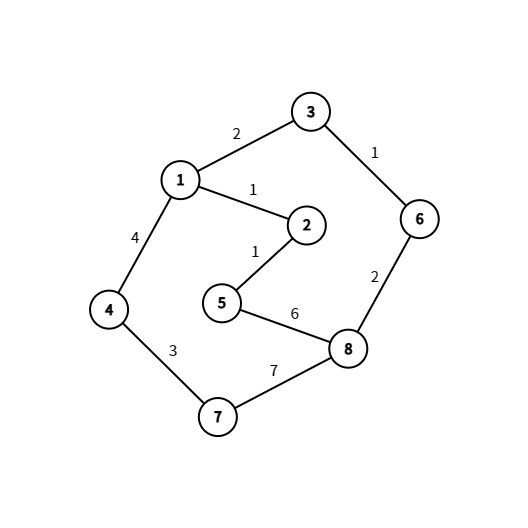
예제 그래프에서 $1$ -> $2$ 간선과 $2$ -> $5$ 간선만 가중치를 $1$로 변경한 그래프이다.
이 그래프에서 $1$번 정점에서 $8$번 정점으로 가는 최단 경로는 $1$ -> $3$ -> $6$ -> $8$로 비용이 $2 + 1 + 2 = 5$이고, $1$ -> $2$ 간선으로 지우면 가중치 $3$만 남기고 모두 지울 수 있다.
하지만, $1$ -> $2$ -> $5$ -> $8$의 경로를 생각해보면, 총 비용은 $1 + 1 + 6 = 9$이지만, $5$ -> $8$ 간선을 추가로 지우면 가중치 $2$만 남기고 모두 지울 수 있어서 이 경우가 최적이 된다.
그럼 이제 어떻게 하면 될까?
나는 BOJ 2206과 비슷하다고 생각했다. bfs할 때 벽을 부순 적이 있는지를 생각하면서 도는 것처럼, 정점 별로 갈 수 있는 최단 경로를 관리할 때, 어떤 간선을 한 번 무시한 적이 있는 경우를 같이 관리해주면 된다.
구현
라이트 모드로 보셔야 잘 보입니다
풀이를 이해하셨다면 구현은 직접 자신의 결로 써보시길 추천드립니다.
# pragma GCC optimize ("O3")
# pragma GCC optimize ("Ofast")
# pragma GCC optimize ("unroll-loops")
# pragma GCC target("sse,sse2,sse3,ssse3,sse4,avx,avx2")
#include <bits/stdc++.h>
using namespace std;
#define fastio ios_base :: sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);
#define all(x) (x).begin,(x).end()
#define fi first
#define se second
typedef long long ll;
typedef pair<ll,ll> pll;
typedef pair<int,int> pii;
typedef vector<int> vi;
typedef vector<ll> vll;
int n,m;
vector<pii> v[5010];
int s,t;
int dist[5010][2];
int main()
{
fastio;
cin>>n>>m;
int sum=0;
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
sum+=c;
v[a].push_back({b,c});
v[b].push_back({a,c});
}
cin>>s>>t;
priority_queue<pair<pii,int>,vector<pair<pii,int>>,greater<pair<pii,int>>> pq;
pq.push({{0,s},1});
for(int i=1;i<=n;i++)
{
for(int j=0;j<=1;j++)
dist[i][j]=1e9;
}
dist[s][1]=0;
while(!pq.empty())
{
auto a=pq.top();
pq.pop();
int cur=a.fi.se;
int co=a.fi.fi;
int flag=a.se;
//cout<<cur<<" "<<co<<" "<<flag<<'\n';
if(co>dist[cur][flag]) continue;
for(auto a:v[cur])
{
int nx=a.fi;
int nx_co=a.se;
if(dist[nx][flag]>co+nx_co)
{
dist[nx][flag]=co+nx_co;
pq.push({{dist[nx][flag],nx},flag});
}
if(flag && dist[nx][0]>co)
{
dist[nx][0]=co;
pq.push({{dist[nx][0],nx},0});
}
}
}
cout<<sum-dist[t][0];
}
그래프 제작 : https://csacademy.com/app/graph_editor
'PS > BOJ' 카테고리의 다른 글
| [백준] BOJ 1733 등번호 (0) | 2024.07.28 |
|---|---|
| [백준] BOJ 22354 돌 가져가기 (0) | 2024.07.26 |
| [백준] BOJ 16000 섬 (0) | 2024.07.25 |
